Lab note #033 Cascading boundary changes in Prolly Trees

Alright, party people. This week I went back to reimplementing Prolly Trees. I wanted to finish out the Lattice Merkle Tree. But given that my goals aren't to just fiddle around in applied research and Prolly Trees already work, I reimplemented Prolly Trees from scratch. I was delighted that the implementation was much cleaner and simpler the second time around. Then the rest of the week was spent exploring its properties.

I start with a simpler implementation first, where we build the tree from scratch, given a list of key-value pairs. But unlike the Fireproof and Noms implementation [^0], I opted to use the Dolt implementation's chunker.

Prolly Trees are probabilistically balanced. It relies on a chunker to determine node boundaries, using the hash of a node as a random variable. In other words, the hash of a node is used as a dice roll, and the chunker uses that to determine whether this is the end of the parent node.

The original Noms threshold chunker looked at the hash of a node, and if it was under a threshold, it would declare it to be a boundary. This maintained a target node size on average, but the standard deviation was quite large. The distribution of node sizes was not normal, instead, it was geometric.

The Dolt Gaussian chunker addressed this by changing how the decision was made. It took both the size of the chunk being built and the hash of the node into account: as the size of the chunk gets bigger, we increase the probability of declaring a boundary. With the right cumulative distribution function, this resulted in a normal distribution for node sizes.

That's great, but there's still a problem. Now that the boundary decision relies both on the size of the chunk and the hash of the node, the decisions are no longer independent! A decision to change a boundary can cascade into subsequent sibling nodes.

This means once we insert a key into a node, we might change that node's end boundary. Once that node boundary changes, it might change the node boundary for the next sibling node. This effect can cascade, even with unicit trees. Worst of all, this can happen at every level of the tree.

These are visualizations of two Prolly Trees. The left tree has 50 entries, and the right tree has a new key-value pair inserted in the 5th index in lexicographical order. The before, and after. Each node's hash is shown in parens, like (749e49). Each leaf node has its key shown in brackets, like [  42916 ]. The nodes that are different between the two trees are highlighted in yellow.

Hence, the nodes that changed as a result of the insertion of a single key are the yellow nodes in the right tree.

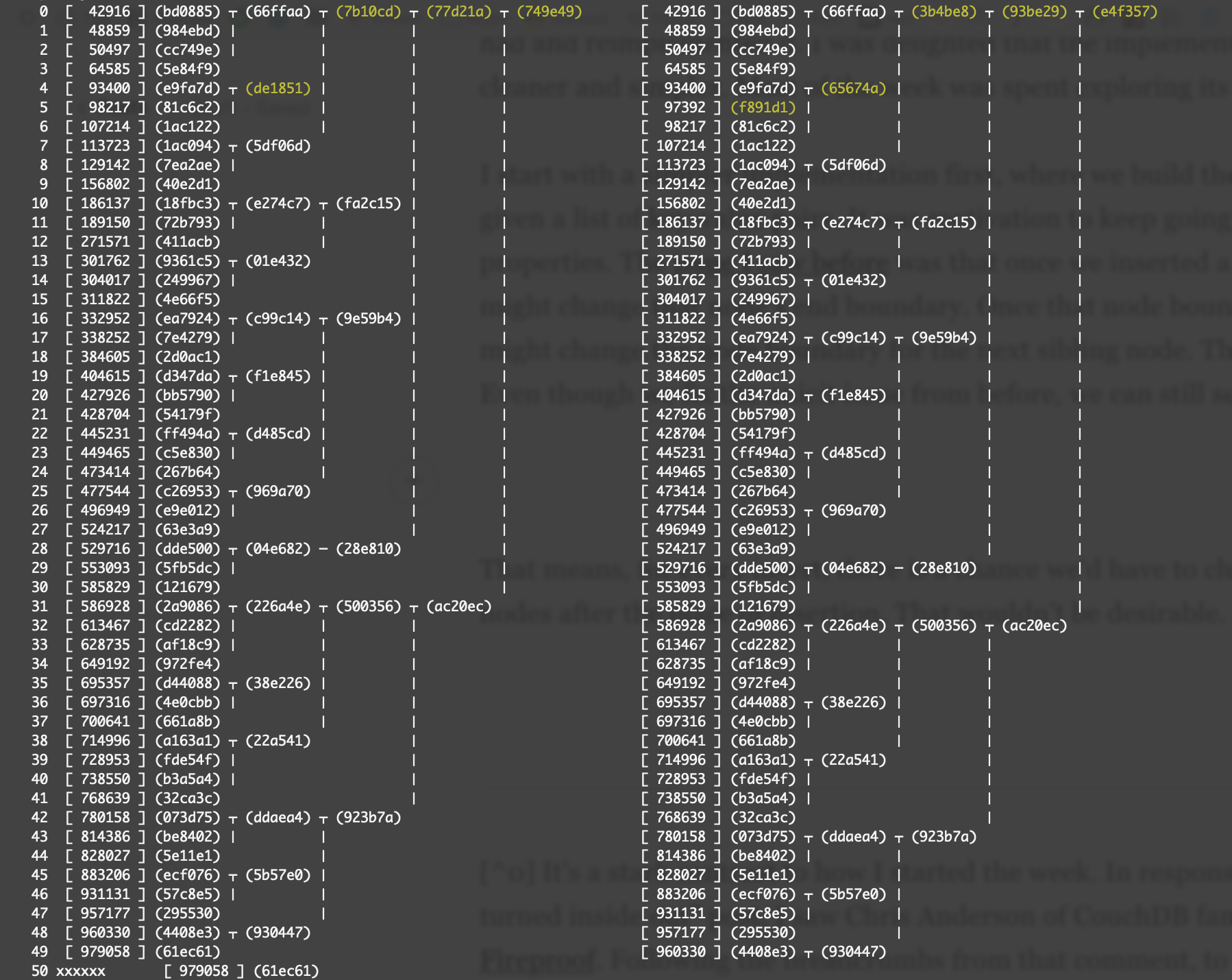
This is the ideal scenario. Inserting key 97392 (f891d1) didn't change the boundary of the node. So the only changed nodes are from the leaf node to the root as a seam. Subsequent sibling nodes of the parent all have the same hashes.

But when the boundary changes as a result of an insertion, boundary changes can cascade. That means, for every insert, there is a chance we'd have to change a whole lot of nodes after the place of insertion. That wouldn't be desirable.

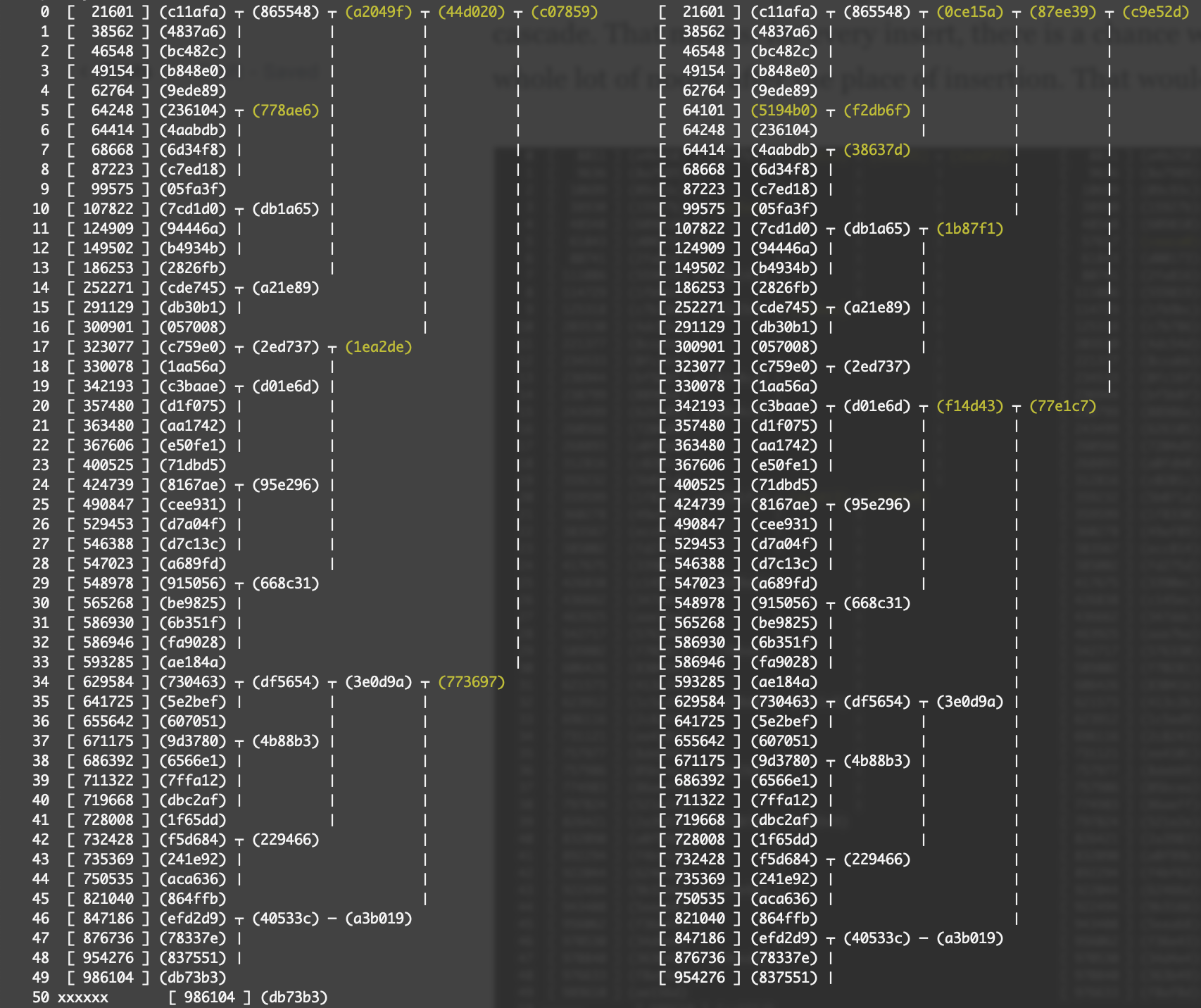
Here, we can see a more pathological case, where inserting key 64101 (hash (5194b0) changed the boundary, so the siblings of the parent node change, and the boundary changes cascade.

How often does this happen? I ran an experiment with the following parameters:

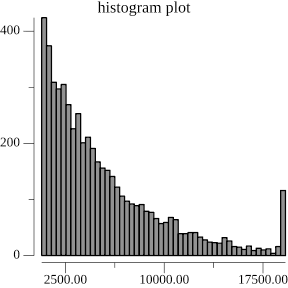
And here's the resulting histogram of the number of nodes that changed.

As you can see, in the typical case, we won't have lots of nodes that change upon insertion. But there's a long tail of up double-digit number of nodes being changed from a single insert. What about as a percentage of the number of nodes of the entire tree?

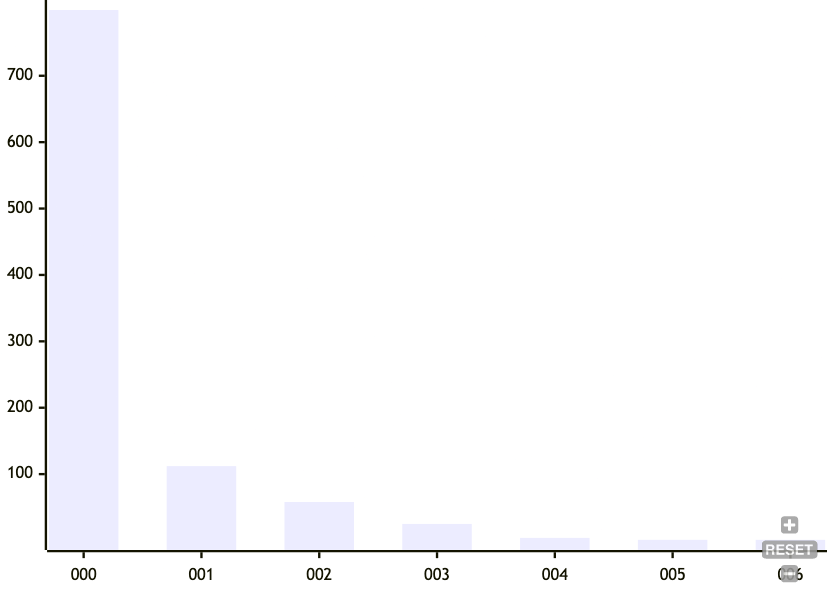
Here, the picture looks a little bit better. Most of the time there aren't a lot of changes. But still, this long tail is bothersome. 5% of a Gigabyte is still 50 Megabytes.

There are two things we can do. We can vary the target mean node size or the target standard deviation of node size. So here's another experiment. First, we'll run the previous one for each target mean node size:

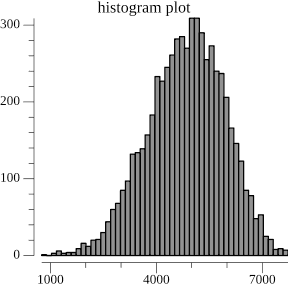
Then we graph the mean number of node changes as a result of a single insertion for all target mean node sizes.

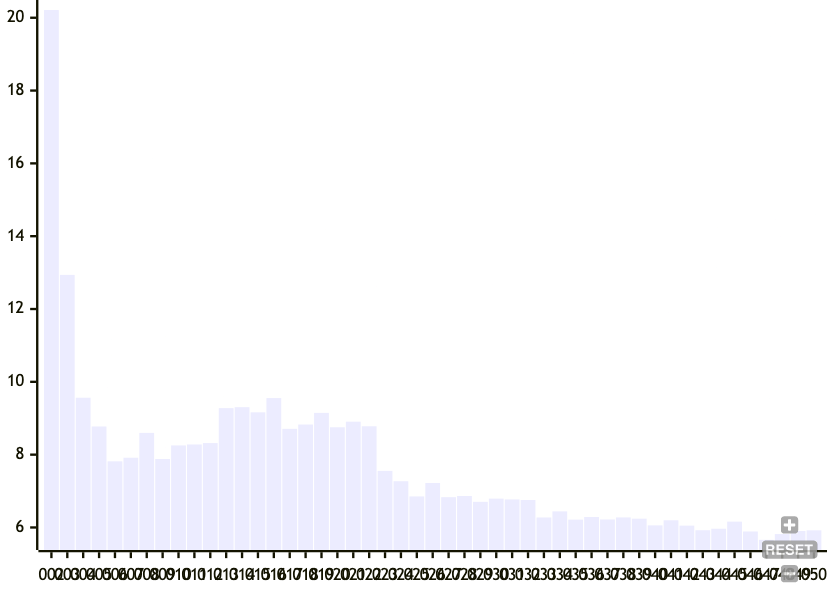
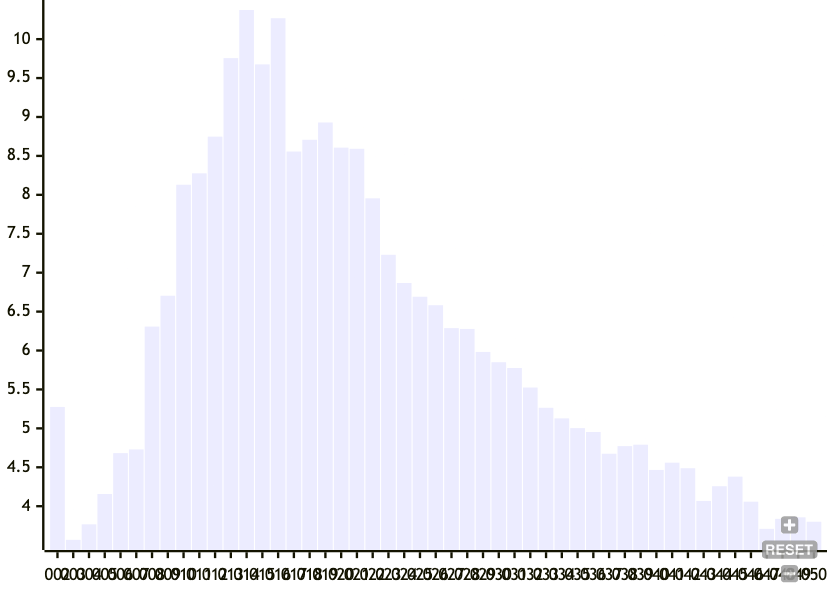
Here, we see that increasing the target node size decreases the number of nodes that change as well as its spread as a result of an insert, at larger node sizes. This does make sense because the larger the nodes the more the chance of a boundary is dominated by the current chunk size, rather than on the hash of the node. But I'm honestly not sure why there's a middle section of target node sizes between 10 and 25 that trigger cascading node changes.

Now, let's vary the target standard deviation of the node sizes.

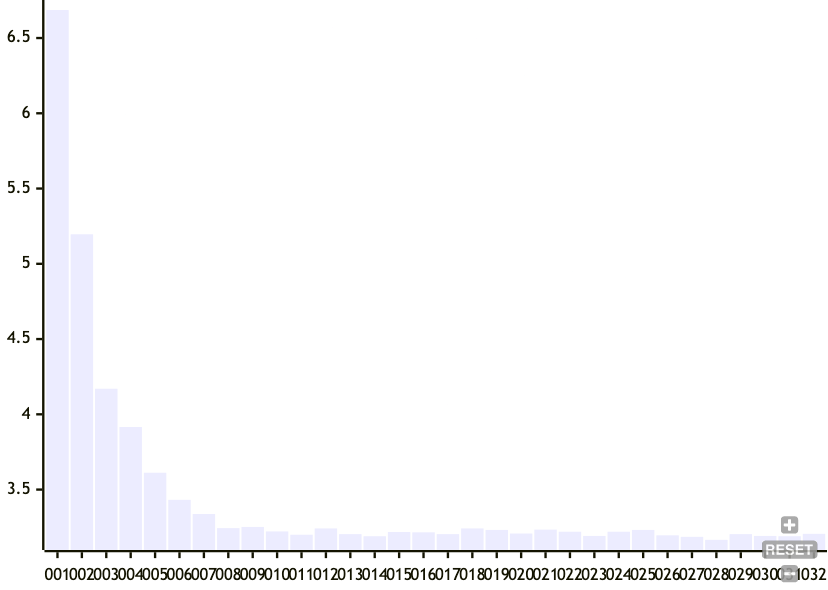
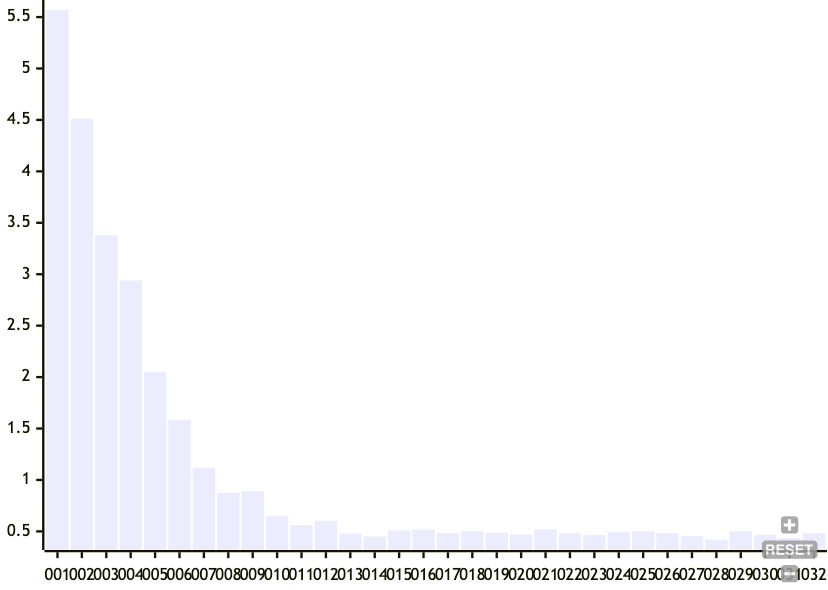
Here, we can see that relaxing the target standard deviation of node sizes is much more effective at tamping down the cascading effect of boundary node changes. This makes sense because if the criteria are relaxed, then the chunker has a lower chance of declaring a boundary as it approaches the mean target node size.

The tradeoff for relaxing the standard deviation of the target node size is a less balanced tree.

For now, this is serviceable and we can tolerate it for what we need to do. So it passes the sniff test for me, and I'll start working on the incremental version of the Prolly Tree. If you have any insightful comments, let me know.

[^0] In response to my "CRDTs turned inside out" post, I saw Chris Anderson of CouchDB fame posting about Fireproof. Following the breadcrumbs from that comment, to "From MLOps to point-of-sale: Merkle proofs and data locality", to the Fireproof Repo ReadMe, then finally to Mikeal Roger's implementation of Prolly Trees.