Lab note #028 Consistent Splitting for Node Sizes

Last week, I was looking at Prolly Trees. A major concern I had was whether the Prolly Tree was unicit [^1], and anhysteretic [^2]. These are desirable properties because it makes comparisons and diffs as easy as comparing the root hash between two trees. Without it, we can be sure that trees are the same if the hashes are the same, but if they're different, we can't be sure whether they're the same or different unless we traverse down the tree to compare the leaf nodes.

A Merkle Search Tree looks for a specific hash with N leading zeros, as a signal to split a node. While this has the expected value of a desired node size, the standard deviation was too big. From a histogram of node sizes by splitting on leading zeros, we can see that the distribution is all over the place.

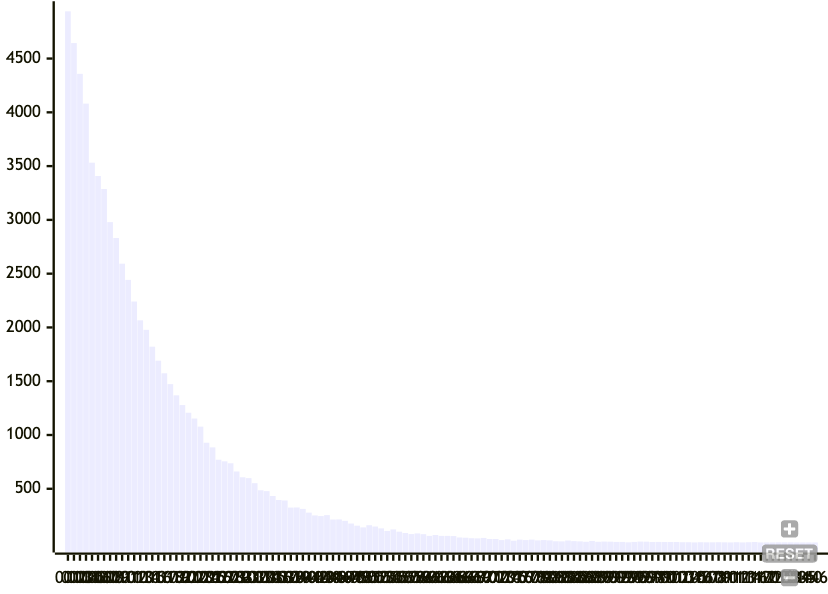
The original formulation of the Prolly Tree uses this same mechanism, so I didn't think it would work well. Instead, I opted for Dolt's mechanism of picking a desired probability density function (PDF), and then using the corresponding cumulative distribution function (CDF) to calculate the conditional probability of a split, given a growing node size. This means that as a node gets bigger, the probability of it splitting gets larger. See previous lab notes for details.

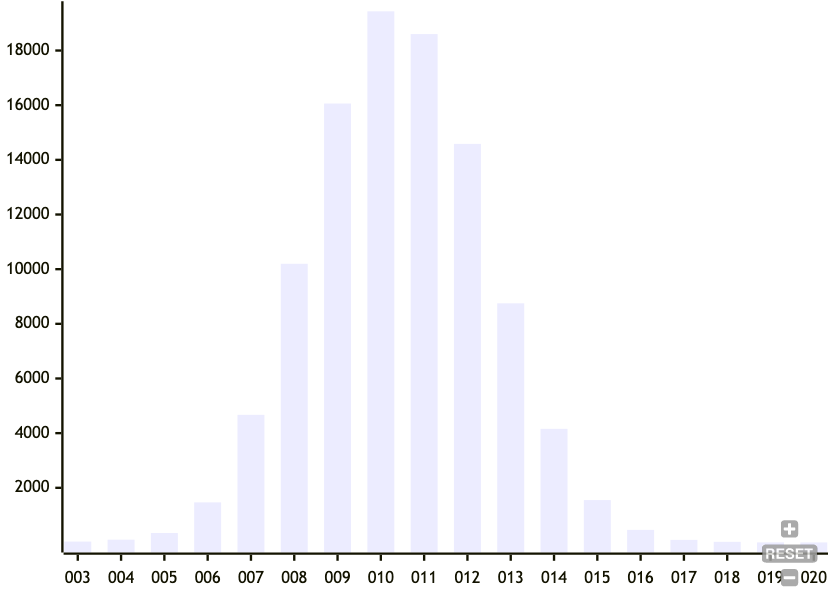
This worked very well in getting a nice standard deviation of node sizes. The problem is that this method isn't unicit and is sensitive to the insertion order.

A little thought and experimentation revealed why. As the algorithm iterates over the list of keys in a node, it decides whether or not to split based on the current key's hash and the number of keys it's decided to pass up. The dependence on the number of keys it's passed up in previous iterations means it's also dependent on the hashes of those keys. Hence, the split decision is sensitive to all previous split decisions, which in turn, makes it sensitive to insertion order.

So we have conflicting goals. Unicity can be achieved if the split decision depends solely on the current key in question. But to get node sizes with less variance, we have to know how many other keys we've passed up.

Admittedly, I'm a little stuck. I currently have two leads. Perhaps there's a way to construct a partial order of splits to construct a semi-lattice, so that they converge to the same splits for the same number of keys under consideration. This is akin to how CRDTs can converge without coordination. But I'm not exactly sure how to formulate it.

The other solution is to accept that there needs to be some kind of balancing on insertion. If there is a split on the current leaf node upon insertion, then we need to check the next consecutive sibling leaf to see if there's going to be a split that differs from the original split decision. If it's not, we can iterate back up the tree. If it is, then we repeat until we potentially reach the far right leaf of the tree. The good news is that the chance of a subsequent split drops precipitously on every split. In the previous lab note, we saw that the chance of a cascading split that's 2 or more sibling leaf nodes away is <4% for a node size of 20. Empirically, this drops to about <1% as node size increases to 80.

So while an insertion has the potential to spike the amount of work to an upper bound of updating the entire right half side of the tree, we can reduce the chance of that happening by increasing the size of the node. Hence, on insert, it will most likely just update the seam from the changed leaf node up to the root. It will be an amortized O(log n) on insert, where n is the number of total nodes, and log n is the approximate height of the tree.

Because there's an apparent solution here that seems workable, I'll likely go with it for the time being and swing back if it turns out to spike performance unpredictably as a garbage collection would. But there's something tantalizingly appealing about a CRDT-like solution to converge node size splits regardless of insertion order. So if you have any ideas about how this might work, feel free to let me know.

[^1] Unicity is where the same set of keys yields the same tree. Since Prolly Trees are a type of Merkle Tree, the same trees would have the same root hash.

[^2] Anhysteretic is where we get the same tree regardless of the insertion order. Or maybe history independence, is a better term.