lab notes

Lab note #027 Breadcrumb to Prolly Trees

Wil

Dec 11, 2023 • 4 min read

When I found the splitting of nodes for Merkle Search Trees to be problematic, I stumbled upon Prolly Trees. They were first described by the Noms, a git for databases. It's a Merkle Tree that can store a sorted set. [^1] Like a B-Tree, all the data is in the leaf nodes, and the branch nodes store the ranges of their child nodes. But instead of pointers to child nodes, Prolly Trees store hashes to child nodes. Prolly Tree node sizes are also not fixed like a B-Tree. Node size is determined by a chunking algorithm that needs to retain three properties for the resulting Prolly Tree.

Consistently unique. Given a set of keys, it will always generate the same unique Prolly Tree. This is called unicity. This makes it easy to compare trees. If the root hashes are the same, then the trees are the same.
History Independent. If the same set of keys are inserted in different orders, it will always generate the same Prolly Tree. This is called anhysteretic. This makes it easy to compare trees when replicating. Even if the keys are replicated out of order, as long as we got all of them, we can be sure the trees are the same.
Minimize cascading splits. If a single key is updated, the chance of splitting the current node and any subsequent leaf nodes in lexicographical order is minimal. This minimizes changes to the tree on updates. If only a single leaf node is changed or split, then only the path up to the root will need to change. The rest of the tree remains unchanged and can rely on structural sharing.

👉

Update: Since writing this Lab Note, I've found that Prolly Trees are likely not unicit, and hence not history independent. Check out the next Lab Note #028 for details.

Prolly Trees have all the advantages of Merkle Trees: easy diffs, verifiable data, and structural sharing. It also has all the advantages of B-Trees: ordered keys, O(log n) retrieval, fit for disk. And unlike Merkle Search Trees, they cannot be attacked by stuffing keys with a hash of leading zeros to raise the tree height.

The traditional Prolly Tree's splitting algorithm in Noms is implemented with a rolling hash with a 64 bit window, sort of like how rsync does it. Dolt takes a different approach. Instead, it has a probability distribution function (PDF) of node sizes it wants to target. It starts from the beginning key for a node, and considers whether it should split or not. For every additional key it considers, it calculates the probability of splitting. The larger the node gets, the more likely it should split. This can be calculated by the cumulative distribution fuction (CDF), denoted as F(x), where s is the currently considered node size, and a is the size of an additional key.

$$\frac{F(s + a) - F(s)}{1 - F(s)}$$

This is a conditional probability. The numerator is the probability a dice roll falls into that interval, and the denominator the the condition in which we're already at the node size. For a normal distribution, the CDF is:

$$ F(x)=\Phi \left(\frac{x-\mu}{\sigma}\right)=\frac{1}{2}\left[1+\operatorname{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right] $$

`erf` is the error function, and can be found in a library or written as an approximation. From the conditional probability, we can construct a threshold that increases for every additional key, and use the hash of the key as a dice roll that decides to split or not. Using that, we find that we get back our target PDF.

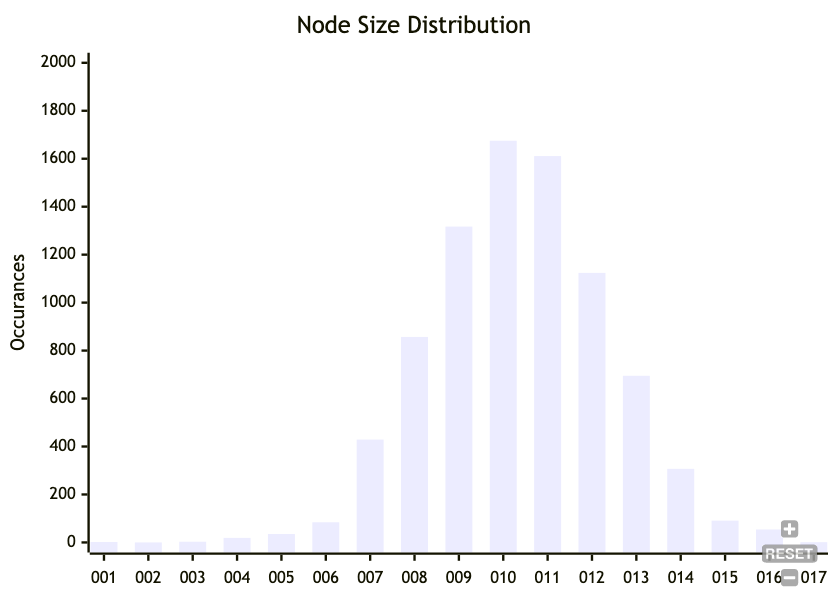
This is for a target normal distribution of 10 keys with a standard deviation of 2 keys. You can also do this for bytes, rather than number of keys. I'm sure there are distributions that have a hard upper limit, so that node sizes don't go above 4KB, so they fit into a page. But I haven't looked deeply into that yet.

One thing I was concerned with was with the chance of cascading splits if a single key was changed.

Generate two streams of keys that differ by a single key in the middle
Chunk both streams, and note the size of each chunk.
Note the difference between size of chunks.
Run for a couple thousand iterations.

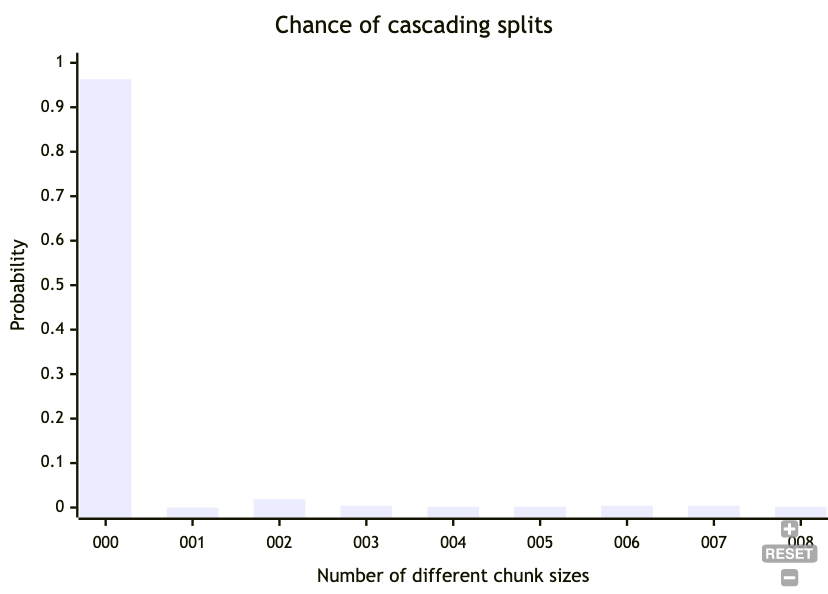
This is for a distribution N(20, 2). We see that most of the time, there are no splits that are different when a single key changes, but occasionally, there will be 1 or more splits that are different. For N(20, 2), 2 or more splits occurs with a probability of less than 0.04.

The larger the size of the node, the less chance of this happening. If we instead count bytes, rather than keys as the size of the node and target 4KB chunks with N(4048, 512), then 2 or more splits occurs with a probability of less than 0.01.

There's more properties I need to verify this next week, such as unicity and anhysteresis, but so far, it seems promising.

[^1] This is now a whole other rabbit hole to fall into. But I did find out Replicache (a player in the local-first space) was founded by Aaron Boodman, the same one working on Noms, who was also responsible for GreaseMonkey.

Sign up for more like this.