lab notes

Lab note #046 Algebraic Effects for Notebook Cells

Wil

• 6 min read
Lab note #046 Algebraic Effects for Notebook Cells

The notebook that I want to build and use has pure functional cells. Functional cells are where the output only depends on the input.

  • No need to figure out the correct execution order for the notebook cells to get it in a working state.
  • For any change, only dependent cells need to be re-executed.
  • Testing is easier because there's no need to specify the entire context before running the cell.
  • Cells can be run in parallel without worry if they trample on the results of others.

However, when building out a pipeline of transformations on data, we often have to fetch and write to data from remote sources. I/O and network is a side-effect because the input/output is now dependent on more than just the arguments to the cell.

Pure functional languages typically deal with side-effects in two ways: with monads or an effects system. [^1]

An effects system is where any side-effect is not executed directly by the user but instead is executed by an underlying system. When a side-effect is raised, a data representation of that side effect is created to be passed around as a first-class value. The user function that raised the side-effect is still considered pure, because the side-effect isn't executed when it's raised, but instead generates the same data representation of the side-effect.

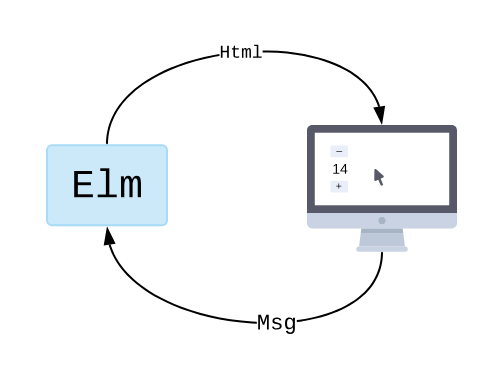
Languages like Elm have an effects system, where any side-effect need to be represented as composable Cmd and Msgdata types that you pass back to the runtime as a return value from the top-level function representing your entire program. This works for Elm because the underlying runtime is in a constant loop with your program. Your program generates data representations of HTML and side-effects you want to render and run, and it gives you back the HTML and the results of the side-effects.

https://guide.elm-lang.org/architecture/

Algebraic effects are a little different. Instead of explicitly passing the side-effect data value explicitly as a return value for the user-written function, side-effects are raised and thrown. When a user-written function wants to perform a side-effect, it "raise/throws a side-effect", much like how we raise/throw an exception. Like exceptions, it skips the rest of the computation and bubbles up the call stack, looking for the nearest handler that can handle the side-effect. But unlike an exception, a handler can jump back to when the side-effect was raised and resume the rest of the computation.

Unlike the Elm runtime, you (the user) can also write how the side-effect is handled. This allows a degree of fine-grained control over control flow that you don't normally see in programming languages. If the typical stack-based calls is driving automatic, algebraic effects is driving stick.

Algebraic effects can be used to implement control flow constructs that are typically out of reach in users in a programming language, such as exception handling, coroutines, async/await, and generators/streams. These are typically language-level constructs assumed as basic building blocks in a language. Algebraic effects are generalized program structure that lets you build your own.

If this seems weird, then rest assured, if you're a web developer, it's likely you've already used them before. React hooks are actually a weak form of Algebraic Effects.

All this to say, I think notebooks would benefit from being purely functional, but with the ability to perform side-effects. There are definitely things to think about and work out, such as maintaining functional purity when an external API endpoint is fetched. But I think the approach is promising because, with algebraic effects, you now can handle the raising of a side-effect differently based on context, while retaining the purity of the function raising the side-effect.

If a side-effect's job is to send an email, then the side-effect handler can decide whether or not to actually send an email based on whether it already sent the email. It can resume computation with 'ok sent' either way, keeping the side-effect-raising function functionally pure. It turns sending email effectively idempotent, so you as a developer never have to worry about sending out multiples of the same email, even if the side-effect-raising function is called multiple times.

There are many other things we can do with algebraic effects to make working with these pipeline transformations more operationally simple, and I think this is one of them.

To my knowledge, only Observable notebooks are purely functional, but they seem to be focused more on visualizations, rather than as a pipeline for data transformations that need to invoke side-effects.

My work this past week was to reload all of this into my head, and then figure out how an implementation works. After some research, it seems that the operational semantics of algebraic effects are based on delimited continuations. Continuations were always confusing to me the way they were described–as a way of saving context and time-traveling back to the past. It's actually just call-stack manipulation beyond the typical push and pop.

In the normal course of executing structured programs, if a first function calls a second function, the call stack grows by pushing the data frame for the second function onto the call stack. When the second function returns, the call stack pops its data frame off of the call stack. With delimited continuations, you can manipulate more than the top of the call stack, and reorder it to your liking. I asked Claude to draw me a picture.

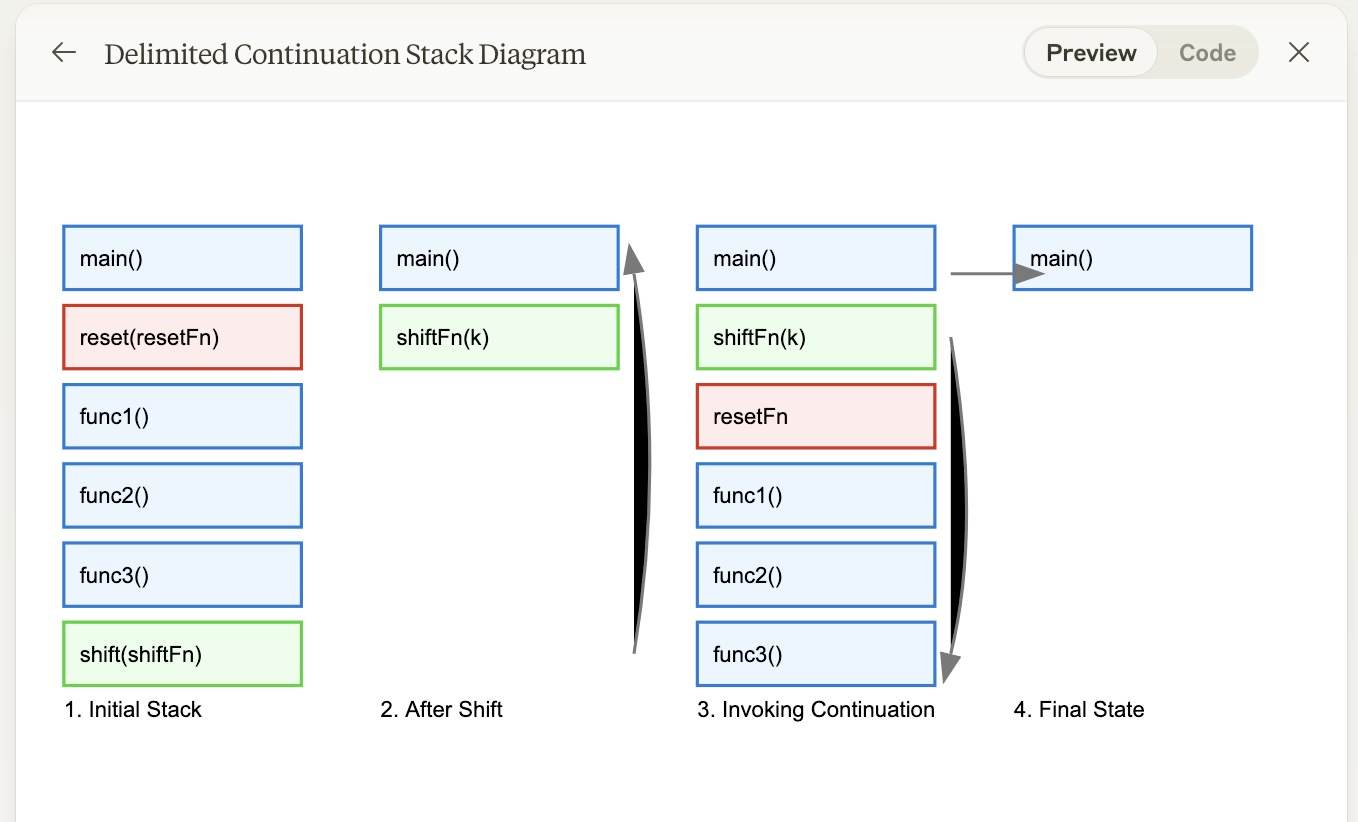
https://claude.site/artifacts/66fc86f9-51df-44a6-88db-4b6b9565b486

Here, we had already set a "save point" at the red stack frame for the function resetFn of the call stack before we called func1 through func3.  When we get to the green function, we invoke the continuation. That means the rest of the computation, resetFn through func3 is skipped, and you can see that in step 2.

This is the equivalent of raising an exception or raising a side-effect. With exceptions, that's the end of the story, and we can only go back to main. With delimited continuations and algebraic effects, we can put the rest of the computation ( resetFn through func3) on top of the green stack frame, and resume execution.

Continuations are just a way to reorder your call stack. With that conceptual frame in mind, it's easier to see how it can be used to implement algebraic effects, and how it is a general structure to implement other control flow mechanisms usually implemented at the language level. It's simply more operators for call stack manipulation beyond push and pop.

There's more that I can say about it, such as what is actually algebraic about algebraic effects? But I think this is probably a good stopping point.

If you want to learn more about them yourself, here's a link dump from my notes. Since many of the current sources stem from research, it can be a bit math-heavy. You can still read them by uploading them into GPT-4, Claude, or NotebookLM and have them explain the paper to you:

If you want just an intro, start here:

This is an unorganized random smattering of bookmarks from my notes:

If you have insights into some nature of Algebraic Effects, feel free to reach out. I'm still learning about them.

[1] I won't go into Monads, but I recently read something that I thought summarized the point of monads well:

That's what "Monads are programmable semicolons" meant. Never clicked until now. Pure functional languages don't have as strict of control flow, due to laziness. Monads claw that control back. It addresses issues that arise in pure functional programming, which result from imposing constraints to achieve desirable properties in programs.
- From The Death of Monads? Direct style Algebraic Effects.

Sign up for more like this.

Enter your email
Subscribe