Lab note #037 Replacing a swath of nodes

The punchline first: the incremental insert is finally done on the Prolly Tree. I don't think I've ever spent so much time on such a small, core piece of code. It was also a lesson for me to lean into the struggle and talk about it.

Last time, I talked about the initial problem of doing a bottom-up breadth-first traversal. I recently just ran into this survey paper on skiplists, which seems like it might be a better fit for layer traversal, but I haven't had the time to look at it yet.

This time, I'll talk about the next tricky bit, replacing nodes once splits were decided upon in a layer.

The incremental insertion of a Prolly Tree differs from the full from-scratch-build in the number of nodes that need to be touched. The path from the root node down to the leaf node that received a new entry is what I call the seam. Every node to the left of the seam doesn't need to be touched, because Prolly Trees are constructed from the left to right.

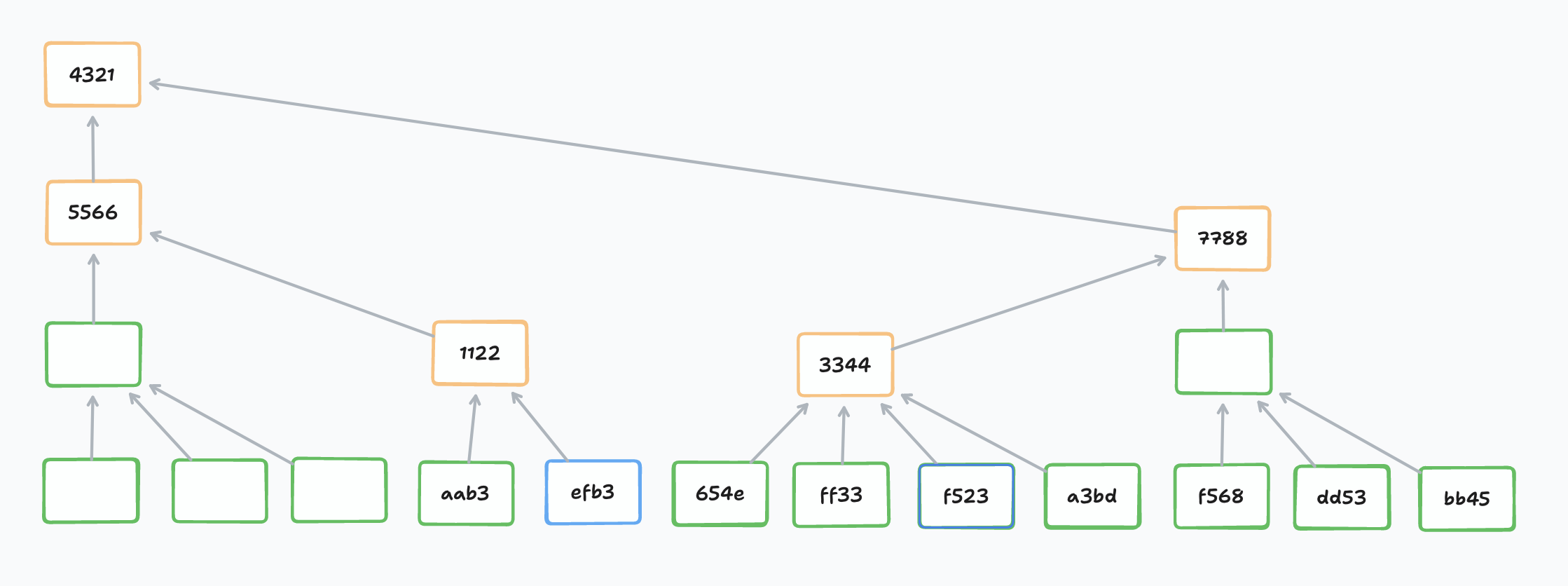
How about nodes to the right? With the new entry, we start finding node boundaries in the layer. The nodes may or may not be grouped as they were before, but eventually, we would find a node boundary that is the same as it was in the previous tree before the insert. Hence, every node to the right of this sync point also does not need to be touched. We do this for every layer.

So between the seam to the left and the sync point to the right, we have a swath of nodes that are grouped into new nodes that need to replace the parent nodes. The tricky bit is, which parent nodes should our new nodes replace?

It's not a one-to-one correspondence because nodes can merge or split, but it is made easier that the nodes need to be replaced in a continuous swath. Hence, we just need to detect the starting point and the ending point.

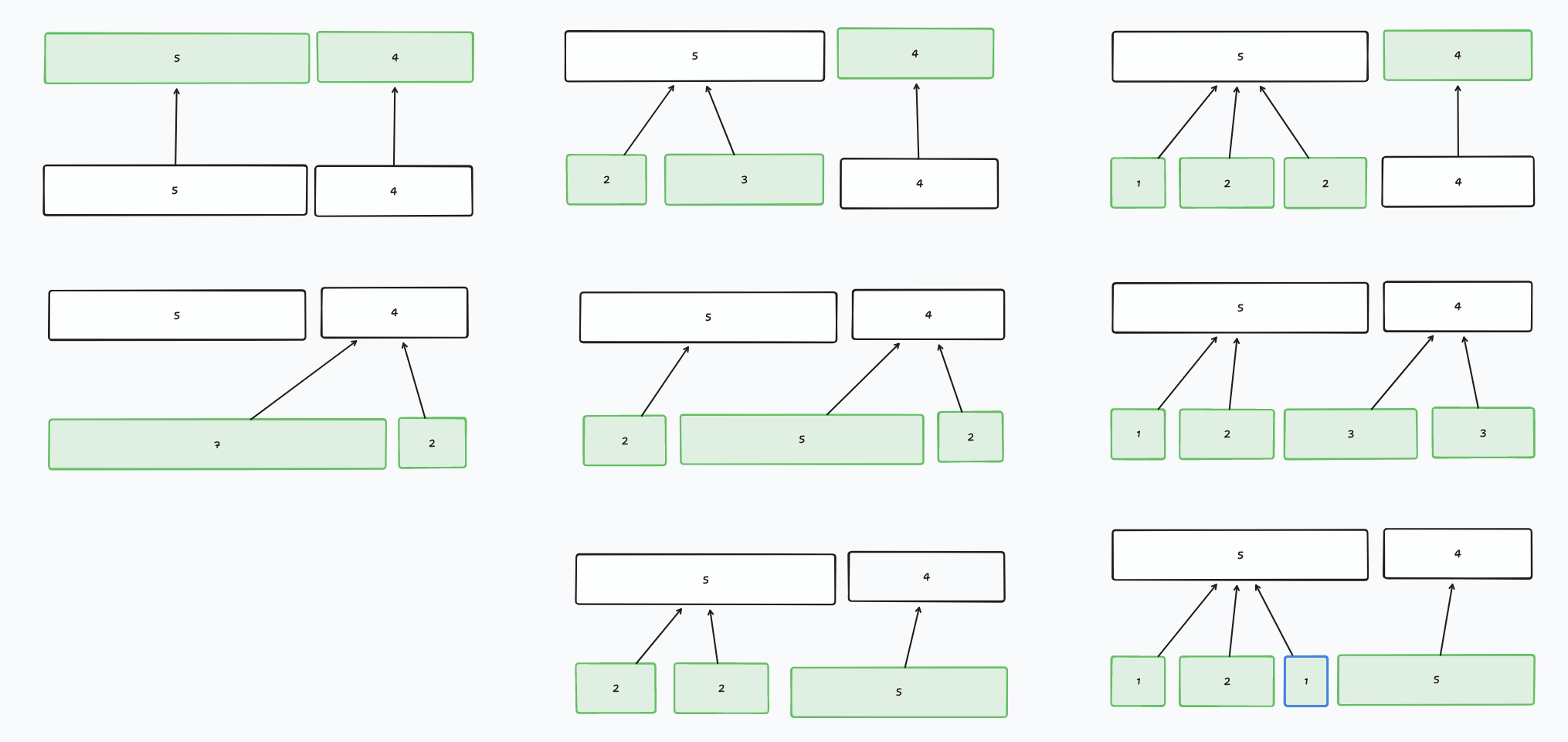
Detecting the ending point is easy. This is the sync point When we find a boundary, we group the nodes since the last boundary and calculate its hash. If it matches the hash of the node we're iterating over (breadth-first-search-wise), then we're done. The edge case in this instance is if we've reached the end of the layer and we didn't find a boundary for the last set of nodes not yet grouped.

But detecting the starting point has edge cases. It's not always the seam, because the new node may or may not end up being grouped by itself. At this point, I still don't quite have a unified clear "theory" of finding this starting point. I wrote a fuzzer that generated 100k random trees, looking for cases where the incremental build didn't match the from-scratch build. Most of the time was spent finding the last 15% of cases and handling them without breaking the previous cases. While writing this, I thought of a different way to do the replacement, but I won't go down that rabbit hole for now.

Dolt recently posted a well-written overview on Prolly Trees. However, they didn't cover the issue of rebalancing upon insertion, which is where the complexity I was wrestling with comes from. When I looked at their codebase a couple of months back, I knew that they addressed it. But it's just not addressed in the post.

Lastly, I didn't find a good way of detecting whether I was back at the top of the tree, because the tree can grow or shrink in height just depending on the boundary conditions, so the depth count isn't reliable. Just looking at whether there is one node to replace isn't a good measure either, because there are branches that could have a single child as well. The easiest solution I found was, after we finish updating the tree, we prune the root if it's got a single stem. It's a bit wasteful, but it works, and it's a small amount of work compared to building the tree incrementally.

Throughout this process, I just felt like I was in this quagmire and never getting out. There was more than one time when I thought I was close to finishing but would run against an issue and would have to roll back a design decision or roll back. Nothing discourages like Hope.

Even worse, when I wasn't making progress, I'd shy away from giving updates, such as writing this newsletter. When I look back, I've noticed this as a recurring pattern. When I butt up against something hard, I knuckle down and try to break through, instead of asking for help or letting others know that I'm struggling. And usually, I do break through, and I learn something. But because it's rewarded time and again, I don't work fast because of it. This is something I'll need to change going forward.

So yes, that means more regular newsletters, even if I didn't make progress. In fact, that's why these are lab notes. They document the successes and the struggles.