lab notes

Lab note #035 A quagmire of replacement nodes

Wil

Feb 12, 2024 • 3 min read

I've been stuck on the incremental insertion of a key in a Prolly Tree, and feeling like I'm in a bog. The version where a Prolly Tree is built from scratch was relatively straightforward. I was able to write it in a day. The incremental version has undergone four or five different revisions. I've lost count. It's tricky in ways I hadn't expected. There were edge cases I didn't anticipate, and my design decisions contributed to increasing code complexity to the point where I'd confuse myself.

💡

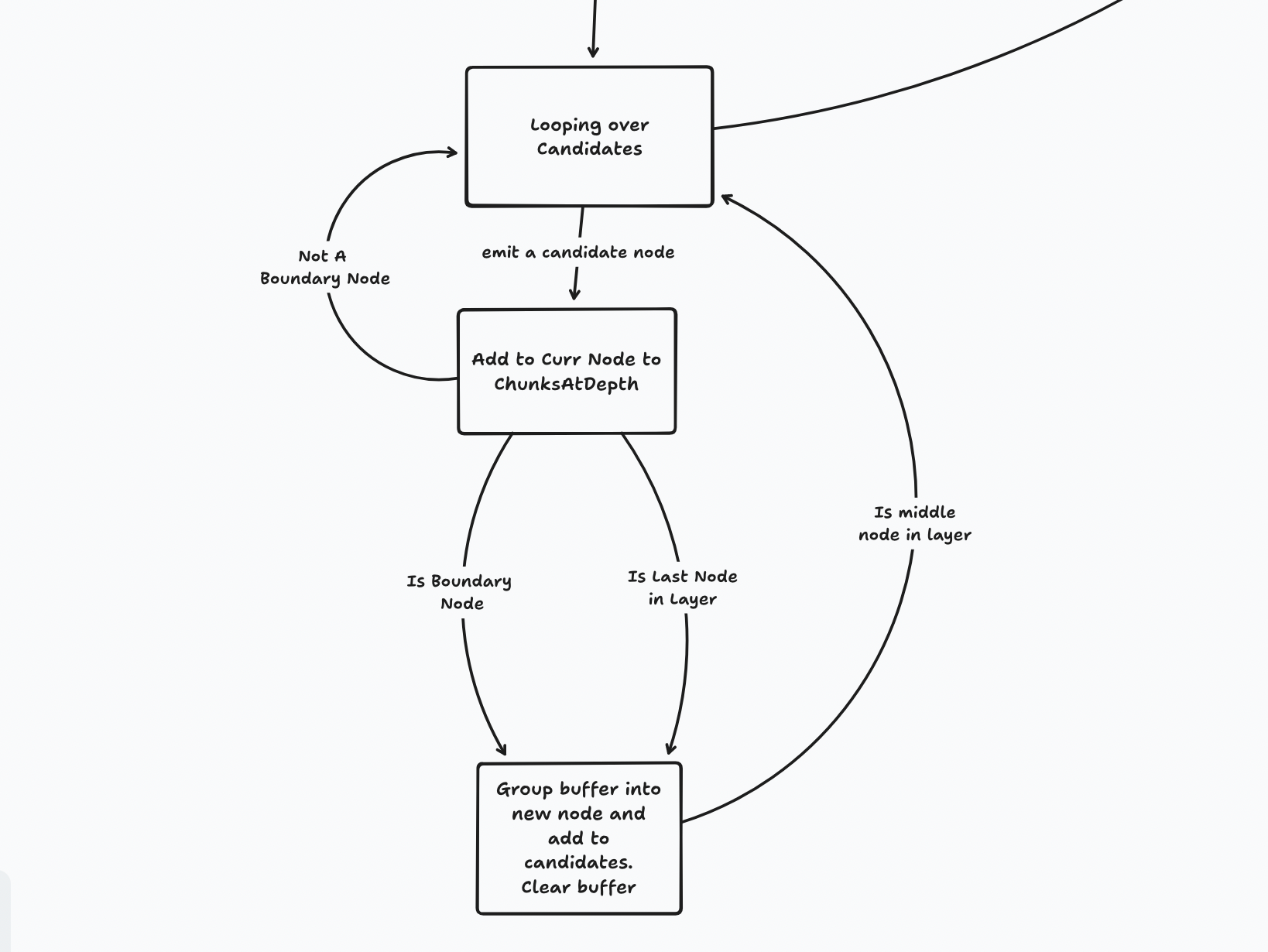
To review, a Prolly Tree is constructed from scratch by processing an ordered list of key-value pairs, splitting them into groups at boundary nodes. Each group becomes the children of a node in the layer above. We repeat until we reach the root node.

In the incremental version, we must traverse the seam down from the root to the target leaf node. Every node to the left of this seam in this layer would be unaltered so we can skip them all. Starting from the left-most sibling of the target leaf node, we start grouping nodes into children for a replacement parent node. We stop when we create a replacement node that has the same hash as the parent. All nodes to the right can be ignored. Repeat on the next higher layer until the root.

Things that caused difficulty:

Only traversing down to the leaf nodes instead of down to the key-value stores meant processing children nodes when one traverses to a node. It was confusing to think of two layers at the same time. Instead, it's much easier to consider a single layer at a time.
Once new replacement nodes were calculated from the current layer for the next higher layer, how do we find the points in the higher layer to replace the nodes?

The second proved tricky because Prolly Trees are also self-balancing. This means upon insertion, there can be splits and merges to node membership in parent nodes. Hence, there's not a one-to-one correspondence between new replacement nodes and the nodes in the parent layer they're meant to replace.

Furthermore, it's not enough to just replace the nodes that have changed. We need a wider swath of nodes than the target seam to the synced node (the first node with the same hash as the initial tree to the right of the seam). Instead, it has to start with the left-most sibling node of the seam to the right-most sibling node of the synced node. This is so we can generate the right hashes.

State machine diagram to detect where to replace parent nodes. This design didn't stick.

How could I have iterated quicker? I think the key this time around was to notice when I'm confused.

Noticing You’re Confused is a technique from the rationalist community where you train yourself to recognize even a slight feeling of confusion as a valuable signal that something about your model of the world is wrong.
https://arr.am/2020/01/23/noticingconfusion/amp/

Normally, I'm able to work out my confusion just by writing and executing code. There's a clarifying amount of detail you can work out only in code. However, I found myself confused because I kept running into details that I hadn't considered when I was just thinking about, as mentioned above. I should stepped back and started drawing diagrams.

Things started clearing up when I started drawing state transition diagrams. And I could see how certain state machines just wouldn't work without writing out the code.

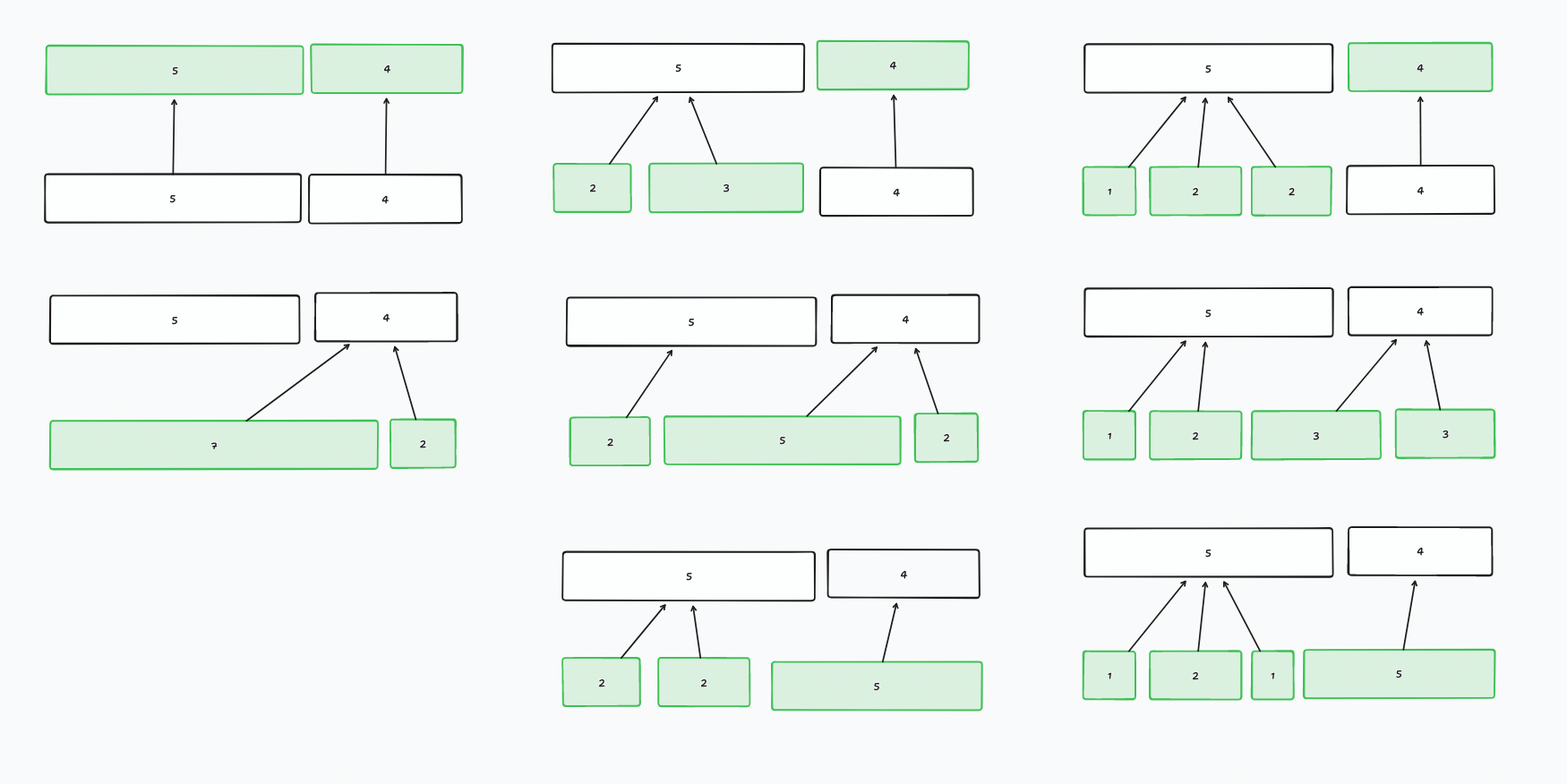
Variations on how different splits might be associated with the parent node that needs to get replaced. This design also didn't survive.

As I've iterated through these different solutions I've simplified it further, but I'm still not at the end of the tunnel. Hopefully, this week will bring an end to this. Must persevere.

Sign up for more like this.