CRDTs Turned Inside Out

Last time, I discussed the trade-offs between more traditional CRDTs, such as the State-based CRDT, Op-based CRDT, and Delta-based CRDT.

There is another class of CRDTs: Merkle CRDTs.

Most ink spilled on CRDTs focuses on consistently merging data from different replicas. That's just half the story. Without a way of storing when concurrent edits happen, merges can't make consistent decisions about conflict resolution.

Normally, this is the job of version vectors in State-based CRDTs and the log of causal operations in Op-based CRDTs. But if you're familiar with blockchains or Git, we notice that Merkle Trees and DAGs (Directed Acyclical Graph) can also do the same job.

The following is how we construct this bookkeeping, exposed as an inherent structure of the concurrent state, rather than hidden away within a container. Let's look at the two variations:

• Merkle-DAG CRDTs
• Merkle Search Tree CRDTs

Merkle-DAG CRDT

The Merkle-DAG (Directed Acyclical Graph) models CRDTs as a growing DAG of Merkle nodes about concurrent updates as events occur. This is a Merklized version of Op-based CRDTs, where the internal bookkeeping grows with the number of state updates, rather than with the number of replicas.

Each node in the Merkle-DAG can carry a payload of operations, state snapshots, or even deltas. This node payload must be a CRDT for the Merkle-DAG to be a CRDT. However, these payload CRDTs can be much simpler in their implementation because the bookkeeping on concurrent edits is delegated up to the Merkle-DAG.

It's as if a state-based CRDT was turned inside-out. The common bookkeeping elements are now the container (the DAG), and the payload-specific bookkeeping is inside of the payload CRDT.

Beyond simpler bookkeeping for payload CRDTs, Merkle-DAG CRDTs have an advantage that non-Merklized CRDTs don't. They can determine equality by comparing root hashes, and they can determine diffs by walking down the DAG.

This reduces the bandwidth for syncing between replicas.

1. A remote replica broadcasts its root hash to our local replica.
2. The local replica compares its root hash with the remote hash to determine if something has changed.
3. If the root hashes are different, it then asks the remote replica to send every node hash as it walks down the DAG from the root.
4. When the remote replica sends a hash that the local replica already has, the path from the root to this node is the list of all nodes missing in the local replica.

This is quite a bit of chatter over the network, but the hashes don't have to be delivered in causal order any more. Merkle DAGs are by definition a causal chain of hashes. Hence, the nodes can be reordered at the receiver, regardless of how they were sent, as long as all of the nodes were received.

An upside of keeping the Merkle-DAG is that the data kept by a Merkle-DAG is immutable. It can be reconstructed and queried at any point in history. Immutability means diffs are easy, undos are easy, and provenance can be verified. But again, the downside here is a history of changes that grows with the number of events. However, Merkle Trees uses structural sharing as a form of compression to lower the space cost of storing such a data structure.

Merkle Search Tree CRDT

The second kind of Merkle CRDT is covered in the Merkle Search Tree paper.

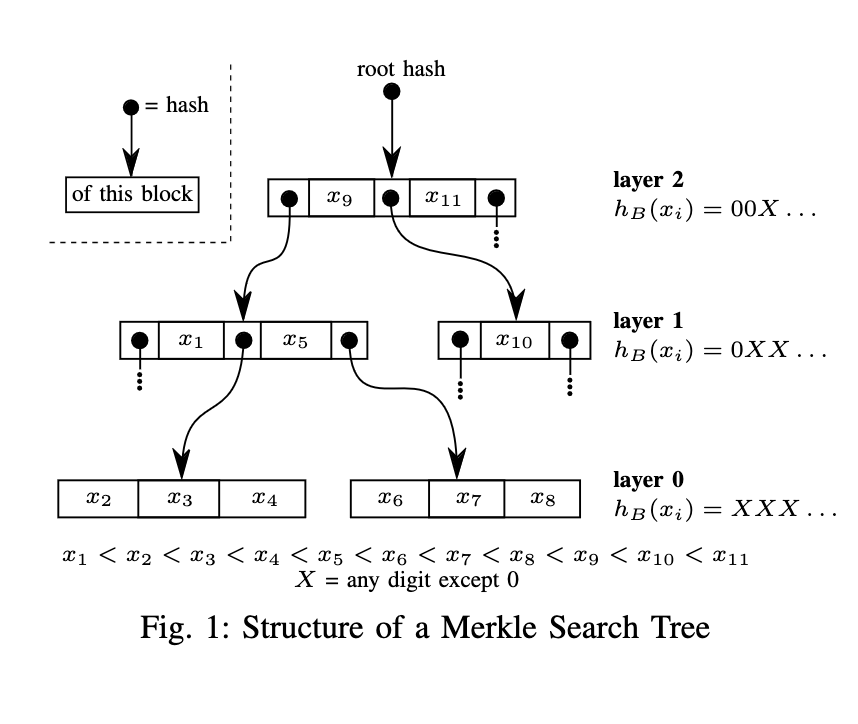
A Merkle Search Tree (MST) is a tree that maintains an ordered set of keys. It does this by maintaining a few invariants.

1. All the keys in a node are ordered.
2. All child nodes between two keys in a node contain entries lexicographically between the two keys.
3. The leaf layer is layer zero. The layer above is layer one, with increasing layer numbers until the root. The layer a key belongs to is dictated by the number of leading zeros in the hash of the key.
4. A node has a content ID that's a hash of all its keys concatenated with the content IDs of all its children. A child node is referenced by its content id.

Keys live in all nodes of an MST tree, unlike a B-tree where keys are only at the leaves. This construction makes MSTs advantageous in two ways: it is self-balancing and it is unicit.

A MST is self-balancing through both invariants #2 and #3. When a key is inserted in the tree, the layer is determined by the key's hash and the node in the layer is determined by the key's value. When the key is inserted in a node between two keys, it necessarily splits the child node between the two keys into two nodes due to invariant #2. Given a hash is in base B and invariant #3, the average number of keys in layer L is B times the average number of keys in layer L + 1. Hence, the average node size is B. Due to the placement of a key being completely deterministic, the tree self-balances.

Unicity means, for a given set of keys, the MST is unique. It implies the MST's construction does not depend on the order of the keys that were inserted. This is extremely desireable, because we can tell if two MSTs are different simply by comparing their root hashes regardless of the insertion order. If the root hash is the same, then the two trees are the same.

To construct a CRDT out of an MST, we simply add a payload to each key that's also a CRDT. Since the MST is an ordered set, merging sets have well-defined semantics, and merging the payloads is delegated to the payload itself to resolve.

And just like the Merkle-DAG construction, the payload CRDT doesn't need to be as complicated. For example, to construct a Grow-Only CRDT, we select the set { ⏊, ⏉ } (called "bottom" and "top" respectively) as the payload CRDT. All the values of the payload start as "bottom" by default. Merging means taking the max of "top" vs "bottom" (top always wins in a max operation).

Unfortunately, the paper leaves out the construction of other CRDTs using MSTs, as it was left as an exercise for the reader. However, there are two other possible constructions I think will work.

Causal Length CRDTs for add-remove sets could be implemented in MSTs with ℤ (the set of integers) as the payload. If the number is even the key doesn't exist, and if it's odd, then it does. Merging would just be taking the max of the two replica's payloads.

Replicated Growable Arrays (RGA) could be implemented by using virtual pointers concatted with the replica ID as the key. Since the MST keeps the keys ordered, we can read back the string by traversing in key order. This would need a mechanism outside of the MST to insert and assign tombstones for deletions. [^3]

Beyond that, there is an undetailed edge case. What if the key you're adding has a lot more (or a lot less) leading zeros in its hash than the number of leading zeros in the current root layer? Do you just add nodes in between the root and the new node? What should go in those in-between nodes? If there are no keys in these in-between nodes and just child content IDs, there would be no way to discern which child to descend into on a query. My guess is to simply insert a ghost key that doesn't exist in the set but only serves as a range bookend for queries. There are implementations to check out for details. [^4]

As for downsides, it's also vulnerable to attackers constructing a key with a large number of zeros and trying to insert it. That would result in a tall tree, reducing queries from O(log n) to O(n). And while the node size is on average B, the variance is spread pretty wide, so it can be common to have nodes that are too small or too large.

The surprising connection

After this and the previous survey on CRDTs, I came away with some clarity on them.

CRDTs need two main ingredients to work, a merge/application operator that's commutative and associative, and some bookkeeping to keep track of concurrent or causal edits. This bookkeeping is like an uncollapsed superposition of state while the system isn't sure if there are any more concurrent edits. If we can be sure that all replicas are synced, we can either collapse the state or simply throw it away if we don't need to travel back in time.

For typical CRDTs, this bookkeeping is internal, and you're given an interface to set and query, so one can pretend this is a regular state that can be updated in place. Merkle CRDTs turn this inside out, exposing the inherent structure of concurrent edits and uncollapsed state for users to see and exploit.

This mirrors closely with how Git is structured. That surprised me at first. But as I dove into Git's history, I found this tidbit in passing.

The important part of a merge is not how it handles conflicts (which need to be verified by a human anyway if they are at all interesting), but that it should meld the history together right so that you have a new solid base for future merges.

In other words, the important part is the _trivial_ part: the naming of the parents, and keeping track of their relationship. Not the clashes.
Linus Travolus vs Bram Cohen

The values are the contents of the file, and the bookkeeping on concurrent edits happens outside of the value. What stops Git from being a CRDT is that its default 3-way merge isn't commutative and associative.

As history proved, it's the bookkeeping data structure that's important for merges, not the conflict resolution itself. But in the case of CRDTs, it's important to constrain the merge with algebraic properties [^2].

The search continues

Merkle Search Trees have lots of nice properties, such as unicity, self-balancing, and a CRDT that doesn't grow with the number of replicas or events. But I think we can do better. For one, the variance of the node sizes is large in MSTs, which makes for uneven trees.

In my search, I found Prolly Trees, and will take a look at them. If anyone has other suggestions for data structures to look at to implement composable CRDTs, let me know. In the meantime, subscribe or follow me on twitter.

[^1] If you aren't familiar with the internals of Git, I'd recommend looking into it.  Git is the only piece of software where learning its internal data structure made it easier to use.
- Git Internals: Plumbing and Porcelain
- A Visual Guide to Git

[^2] The algebraic properties we need to maintain for a merge are commutativity, associativity, and idempotency. This forces every replica to arrive at the same merged state without coordinating with each other.

[^3] Of course, actual RGA implementations are far more optimized than this outline.

[^4] There are two existing implementations of MSTs.

• https://github.com/domodwyer/merkle-search-tree
• https://github.com/jrhy/mast